学而思奥数天天练栏目每日精选一套高等难度的试题,各年级分开,配有详细答案及试题解析,此类试题立足于杯赛真题、综合应用和加深各知识点,适合一些志在竞赛中夺取佳绩的学生。
·本试题由武汉学而思奥数专职教师王帅老师精选、解析,以保证试题质量。
名师介绍: 毕业于北京师范大学数学与应用数学专业,小学数学奥林匹克二等奖,全国初中数学联赛市级一等奖。
教学特色: 王帅老师,富有青春活力,热爱教育事业,讲课生动形象,注重引导孩子养成良好的学习习惯。王老师对学生非常有爱心和耐心,善于调动学生学习的积极性,抓住学生思路和心理,引导学生思考,锻炼孩子自己动脑解决问题的能力,在讲课中能及时与每个学生沟通,善于发现每个孩子身上的优点,帮助他们建立学习兴趣和信心,培养他们严密的逻辑思维能力,找到适合每个孩子自己的学习方法,用生动有趣的语言配合细致的讲解,带领孩子们一步步成长。
·每道题的答题时间不应超过15分钟
·您可以按“点击下载适合打印版本试卷”获得word版本试卷进行打印
小学一年级天天练答案:
因为14+7-4=17,要使等式右边等于11可以采用多减、少加的办法。通过改变运算符号就可以达到多减少加的目的。
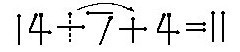
小学二年级天天练答案:
解:用数字代表盘子里的苹果数,用由3个数字组成的数组表示不同的放置方式.如(7,0,0)表示:一个盘子里放7个苹果,而另外两个盘子里都空着不放.各种可能的放置情况如下:
(7,0,0)
(6,1,0)
(5,2,0),(5,1,1)
(4,3,0),(4,2,1)
(3,3,1),(3,2,2)
数一数,共有8种不同的放法.
小学三年级天天练答案:
解:题中有"至少"这一条.
用逆推法从最后的最少棋子情况逆推.先画线段图依次表示分棋子的过程,见下图:
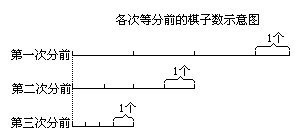
假设第三次分时,三等份中每分是1个棋子(最少),
则此次分前应是3+1=4个;4÷2=2,则第二次分前应是2×3+1=7个,注意7是奇数(第二次分前的棋子是第一次分后的两份,应是偶数所以不应是7,可见前面假设不对).
再假设第三次分时每等份是2个棋子,也不行.
又假设第三次分时每等份是3个棋子,则有
3×3+1=10;
10÷2=5,5×3+1=16;
16÷2=8,8×3+1=25;
∴原来有棋子至少是25个.
小学四年级天天练答案:
分析:已知偶数个奇数的和是144.连续数的个数为偶数时,它的特点是首项与末项之和等于第二项与倒数第二项之和,等于第三项与倒数第三项之和……即每两个数分为一组,八个数分成4组,每一组两个数的和是144÷4=36.这样可以确定出中间的两个数,再依次求出其他各数。
解:①每组数之和:144÷4=36
②中间两个数中较大的一个:(36+2)÷2=19
③中间两个数中较小的一个:19-2=17
∴这八个连续奇数为11、13、15、17、19、21、23和25。
答:这八个连续奇数分别为:11、13、15、17、19、21、23和25。
小学五年级天天练答案:
解解:连结BD,将四边形ABCD分成两个部分S1与S2.连结FD,有S△FBD=S△DBC=S1所以S△CGF=S△DFC=2S1.
同理S△AEH=2S2,
因此S△AEH+S△CGF=2S1+2S2=2(S1+S2)=2×1=2.
同理,连结AC之后,可求出S△HGD+S△EBF=2所以四边形EFGH的面积为2+2+1=5(平方单位)






